lunedì 22 giugno 2015

Legge di Betz

Legge di Betz

Da Wikipedia, l'enciclopedia libera.
Schema di un flusso di fluido attraverso un attuatore.
La legge di Betz mostra la massima energia possibile — conosciuta come limite di Betz — che si potrebbe ricavare tramite un rotore infinitamente sottile da un fluido che scorre ad una certa velocità.
Al fine di calcolare l'efficienza massima di un rotore sottile, lo si immagini sostituito da un disco che spilli energia dal fluido che vi passa attraverso. Ad una certa distanza dietro questo disco, il fluido che vi è passato attraverso fluisce con una velocità ridotta.

  1. Il rotore non possiede mozzo, ossia è un rotore ideale, con un infinito numero di pale e con attrito pari a 0. Ogni attrito risultante può essere solo inferiore di questo valore ideale;
  2. Il flusso all'entrata e all'uscita del rotore ha un moto assiale. Questo tipo di approccio è a volume di controllo, e per ricavare una soluzione il volume di controllo deve contenere tutto il fluido entrante e uscente, in considerazione delle equazioni di conservazione;
  3. Il fluido è incomprimibile. La densità rimane costante, e non vi è trasferimento di calore dal rotore al fluido e viceversa;
  4. Ad eccezione del rotore, non sono presenti altri ostacoli all'interno delle vene fluide che possano alterarne il moto;
  5. La porzione di flusso che attraversa lo specchio dell'attuatore non ha alcuna interazione con la restante parte di fluido che lo circonda e che non interagisce con l'attuatore;
  6. Nelle sezioni a valle e a monte del flusso complessivo vi è uno stato di assoluta calma aerodinamica;
  7. La velocità del fluido è uniformemente distribuita ed il modulo unidirezionale in ogni parte del flusso.

Applicazione della conservazione della massa (equazione di continuità)[modifica | modifica wikitesto]

Applicando l'equazione di continuità a questo volume di controllo, il tasso di massa fluida (ossia la massa fluente per unità di tempo) è data da:
\dot m = \rho \cdot A_1 \cdot v_1 = \rho \cdot S \cdot v = \rho \cdot A_2 \cdot v_2

dove v1 è la velocità davanti il rotore, v2 è la velocità alle spalle del rotore, e v è la velocità all'altezza del dispositivo. ρ è la densità del fluido, e l'area della turbina è data da S. La forza esercitata dal vento sul rotore può essere scritta come
F = m \cdot a = m \cdot \begin{matrix} \frac{dv}{dt} \end{matrix} = \dot m \cdot \Delta V
= \rho \cdot S \cdot v \cdot ( v_1 - v_2 )

Potenza e lavoro[modifica | modifica wikitesto]

Il lavoro fatto dalla forza può essere scritto in forma differenziale come

dE = F \cdot dx

e la potenza contenuta nel fluido è

P = \begin{matrix} \frac{dE}{dt} \end{matrix} = F \cdot \begin{matrix} \frac{dx}{dt} \end{matrix} = F \cdot v

Ora sostituendo la forza F calcolata in precedenza nell'equazione della potenza, sarà disponibile la potenza che può essere estratta dal fluido in movimento:

P = \rho \cdot S \cdot v^2 \cdot (v_1-v_2)

Comunque, la potenza può essere calcolata in un altro modo: usando l'energia cinetica. Applicando l'equazione di conservazione dell'energia al volume di controllo otteniamo

P = \frac{\Delta E}{\Delta t} = \begin{matrix} \frac12 \end{matrix} \cdot \dot m \cdot (v_1^2 - v_2^2)

Tornando all'equazione di continuità, una sostituzione per il tasso di massa fluida ottiene il seguente

P = \begin{matrix} \frac12 \end{matrix} \cdot \rho \cdot S \cdot v \cdot (v_1^2 - v_2^2)

Entrambe queste espressioni per il calcolo della potenza sono valide: una di queste deriva dall'analisi del lavoro incrementale eseguito, e l'altra dalla conservazione dell'energia. Risolvendo queste due espressioni, otteniamo un risultato interessante

P = \frac12 \cdot \rho \cdot S \cdot v \cdot (v_1^2 - v_2^2) = \rho \cdot S \cdot v^2 \cdot (v_1-v_2)

Esaminando le due espressioni equivalenti, principalmente
\begin{matrix} \frac12 \end{matrix} \cdot (v_1^2-v_2^2) = \begin{matrix} \frac12 \end{matrix} \cdot (v_1 - v_2) \cdot (v_1 + v_2) = v \cdot (v_1-v_2)

e quindi

v = \begin{matrix} \frac12 \end{matrix} \cdot (v_1 + v_2)

Pertanto, la velocità del fluido al rotore può essere considerata come una media delle velocità del settore a monte e di quello a valle, a condizione che essi non abbiano velocità uguali (nel qual caso non viene estratta potenza). Questo è spesso considerato il punto di più difficile accettazione della Legge di Betz ma, come si può vedere dalla dimostrazione sovrastante, è in realtà corretto.

Coefficiente di carico[modifica | modifica wikitesto]

Il coefficiente di carico è definito come il rapporto tra la potenza erogata e la massima potenza che può essere ottenuta, ovvero come il lavoro adimensionale:
w*= \frac {P}{P_{\rm max}}
per ottenere tale valore si può partire dall'espressione precedente della potenza basata sull'energia cinetica:
\dot E = \begin{matrix} \frac12 \end{matrix} \cdot \dot m \cdot (v_1^2 - v_2^2)
= \begin{matrix} \frac12 \end{matrix} \cdot \rho \cdot S \cdot v \cdot (v_1^2 - v_2^2)
= \begin{matrix} \frac14 \end{matrix} \cdot \rho \cdot S \cdot (v_1 + v_2) \cdot (v_1^2 - v_2^2)
= \begin{matrix} \frac14 \end{matrix} \cdot \rho \cdot S \cdot v_1^3 \cdot (1 - (\frac{v_2}{v_1})^2 + (\frac{v_2}{v_1}) - (\frac{v_2}{v_1})^3) .

L'asse orizzontale rappresenta il rapporto  \begin{matrix} \frac{v_2}{v_1} \end{matrix} , l'asse verticale è il "coefficiente di prestazione" Cp.
Differenziando, in base alla regola della catena  \dot E  rispetto a  \begin{matrix} \frac{v_2}{v_1} \end{matrix}  per una data velocità del fluido v1 e una data area S è possibile trovare il massimo o il minimo valore che assume  \dot E . In particolare si trova che il massimo valore si ha per  \frac {v_2}{v_1} = \frac13 .
Sostituendo questi risultati nella formula precedente si trova:
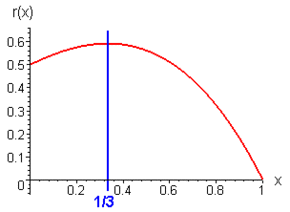
P_{\rm max} = \begin{matrix} \frac{16}{27} \cdot \frac{1}{2} \end{matrix} \cdot \rho \cdot S \cdot v_1^3 .
La frazione di lavoro ottenibile da un cilindro di fluido con area S e velocità v1 è:
P = \begin{matrix} \frac12 \end{matrix} \cdot \rho \cdot S \cdot v_1^3 .
Il coefficiente di carico ha il suo massimo valore di 0.593. Le perdite del rotore in un mulino a vento, per esempio, sono le più significative. È, comunque, importante ridurle il più possibile. I rotori moderni ammettono valori nell'intervallo da 0.4 a 0.5, che è il 70-80% di quello teoricamente possibile.

Punti di interesse[modifica | modifica wikitesto]

Notare che la precedente analisi non è dipendente dalla geometria, pertanto S potrebbe assumere qualsiasi forma a condizione che il flusso attraversi assialmente dall'ingresso al volume di controllo di uscita, e il controllo del volume è uniforme per le velocità di ingresso e di uscita. Notare che ogni effetto estraneo può solo decrementare la performance della turbina poiché l'analisi è stata effettuata ignorando l'attrito. Ogni effetto non ideale andrebbe a detrarsi dall'energia disponibile dal fluido in ingresso, diminuendo l'efficienza.
Ci sono state diverse argomentazioni su questo limite e gli effetti degli ugelli, e c'è una netta difficoltà quando si considerano i dispositivi di potenza che utilizzano più area di cattura dell'area del rotore. Alcuni produttori e inventori hanno creduto di superare il limite di Betz facendo questo ma, in realtà, le loro ipotesi iniziali erano sbagliate, dato che si sta utilizzando una A_1 sostanzialmente maggiore dell'area del rotore, e questo apporta squilibrio al numero di efficienza. In realtà, il rotore è efficiente come potrebbe esserlo senza ugelli o dispositivi di cattura, ma è aggiungendo questi dispositivi che si aumenta la potenza estraibile dal vento a monte del rotore.

Osservazione: Se usiamo la seguente media delle velocità
Vavg=2/(1/V1+1/V2)=2*V1*V2/(V1+V2)
Al posto di Vavg=(V1+V2)/2 poiché V2=0 allora Vavg=0 per qualunque valore di V1 (impatto senza movimento). Il calcolo è molto semplice e dà una riduzione del 50% della produzione.

Bibliografia[modifica | modifica wikitesto]

  • Betz, A. (1966) Introduction to the Theory of Flow Machines. (D. G. Randall, Trans.) Oxford: Pergamon Press.
  • Ahmed, N.A. & Miyatake, M. A Stand-Alone Hybrid Generation System Combining Solar Photovoltaic and Wind Turbine with Simple Maximum Power Point Tracking Control, IEEE Power Electronics and Motion Control Conference, 2006. IPEMC '06. CES/IEEE 5th International Volume 1, Aug. 2006 Pagine:1 - 7.

Voci correlate[modifica | modifica wikitesto]

Pubblicato da alle

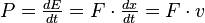
Nessun commento:

Posta un commento

Iscriviti a: Commenti sul post (Atom)